2011/4/2
ティルソンT3移動平均
ティルソンT3移動平均はTim Tillsonによって開発された移動平均で、その実態は3重のGeneralized DEMAです。
短周期でも滑らかな線が得られることが特徴です。
使用する関数
ティルソンT3移動平均は3重のGeneralized DEMAなのですがそのまま3重のGeneralized DEMAを計算するとかなり複雑になるので
式を展開して計算します。
任意の日数のティルソンT3移動平均が計算できるようにOFFSET関数を使います。
計算式を作る前に3重のGeneralized DEMAを展開します。
N日Generalized DEMAはGDEMA(N)と表記することにします。
N日指数移動平均はEMA(N)と表記することにします。
M重N日指数移動平均はEMAM(N)と表記することにします。2重指数移動平均ならEMA2(N)、5重指数移動平均ならEMA5(N)となります。
2重GDEMAは
GDEMA(GDEMA(N)) = EMA(GDEMA(N))×(1+f)-EMA2(GDEMA(N))×f
=EMA(EMA(N)×(1+f)-EMA2(N))×(1+f)-EMA2(EMA(N)×(1+f)-EMA2(N)×f)×f
={EMA(EMA(N)×(1+f))-EMA(EMA2(N)×f)}×(1+f)-{EMA2(EMA(N)×(1+f))-EMA2(EMA2(N)×f)}×f
ここで
EMA(EMA(N))=EMA2(N), EMA(EMA2(N))=EMA3(N), EMA2(EMA(N))=EMA3(N), EMA2(EMA2(N))=EMA4(N)であり
関数内の係数は外にだすことができる、つまりEMA(EMA(N)×f)=EMA2(N)×fとできるので
上記の式を纏めると
GDEMA(GDEMA(N))=EMA2(N)×(1+f)^2 - EMA3(N)×f×(1+f) - EMA3(N)×f×(1+f) + EMA4(N)×f^2
=EMA2(N)×(1+f)^2 - 2×EMA3(N)×f×(1+f) + EMA4(N)×f^2
となります。
この形をよくみると(X-Y)^2の展開式をX=X×(1+f), Y=Y×fとして計算するのと同じ係数が得られることがわかります。
つまり、移動平均の式の展開はそれぞれの要素を簡単なX,Yなどでで置き換えて展開しても同じ係数が得られるということです。
上記の場合だと展開した後にX=EMA(N)、Y=EMA2(N)と置き換えてX^2=EMA(EMA(N))と解釈すれば同様の式が得られるということです。
よって、3重のGDEMAの展開式はX=EMA(N)、Y=EMA2(N)として、{X×(1+f)-Y×f}^3を展開すれば良いということになります。
{X×(1+f)-Y×f}^3を展開すると
X^3×(1+f)^3 - 3×X^2×Y×(1+f)^2×f + 3×X×Y^2×(1+f)×f^2 - Y^3×f^3
となり、X=EMA(N)、Y=EMA2(N)とすれば
EMA3(N)×(1+f)^3 - 3×EMA(4)×(1+f)^2×f + 3×EMA5(N)×(1+f)×f^2 - EMA6(N)×f^3
となります。
これで、準備が整いました。
M3セルはT3移動平均の計算日数を指定するセルとします。
N3セルはfを指定するセルとします。
G列で終値の指数移動平均を計算します。計算式の説明は指数移動平均を参照してください。
H列でG列の指数移動平均(2重指数移動平均)を計算します。同様にI列〜L列で3重〜6重の指数移動平均を計算します。
計算式はそれぞれ左隣の列の指数移動平均になっているので計算式の説明は省略します。
I3セルで3重指数移動平均の係数を計算します。
3重指数移動平均の係数は(1+f)^3で計算できるので式は=(1+N3)^3となります。
J3セルで4重指数移動平均の係数を計算します。
4重指数移動平均の係数は-3×(1+f)^2×fで計算できるので式は=-3*((1+N3)^2)*N3となります。
K3セルで5重指数移動平均の係数を計算します。
5重指数移動平均の係数は3×(1+f)×f^2で計算できるので式は=3*(1+N3)*(N3^2)となります。
L3セルで6重指数移動平均の係数を計算します。
6重指数移動平均の係数は-f^3で計算できるので式は=-N3^3となります。
M列でティルソンT3移動平均を計算します。
計算式はEMA3(N)×(1+f)^3 - 3×EMA(4)×(1+f)^2×f + 3×EMA5(N)×(1+f)×f^2 - EMA6(N)×f^3です。
各指数移動平均の数値はI列〜L列で、各指数移動平均の係数はI3セル〜L3セルで計算してあるので
Excelの式は赤枠内赤字部分
G5〜M5セルをコピーしG6以下のセルにペーストすればティルソンT3移動平均が計算できます。
Excelファイルがダウンロードできない場合はリンクを右クリックして「対象をファイルに保存」を選択して保存すればダウンロードできます。
短周期でも滑らかな線が得られることが特徴です。
計算式
ティルソンT3移動平均={Generalized DEMAのGeneralized DEMA}のGeneralized DEMA
Generalized DEMA = EMA(N) × (1 + f) - EMA2(N) × f
EMA(N)はN日指数移動平均
EMA2(N)はN日指数移動平均のN日指数移動平均
fは0〜1の間の数字で通常はf=0.7とする
Nは任意
Generalized DEMA = EMA(N) × (1 + f) - EMA2(N) × f
EMA(N)はN日指数移動平均
EMA2(N)はN日指数移動平均のN日指数移動平均
fは0〜1の間の数字で通常はf=0.7とする
Nは任意
 |
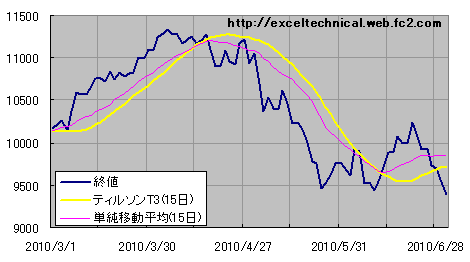日経平均終値とティルソンT3移動平均の図
Excelを使ってティルソンT3移動平均を計算する
Excelを使ってティルソンT3移動平均を計算する手順を説明します。使用する関数
AVERAGE(数値1,数値2,…)
指定した数値や範囲内の数値の平均値を計算する。空白セルや文字列は無視して計算します。OFFSET(基準セル,行数,列数,高さ,幅)
基準セルから指定した行数、列数だけ移動したセルを参照します。または高さ、幅を設定して基準セルから指定した高さ、幅のセル範囲を指定します。IF(条件式,真の場合,偽の場合)
条件式を満たす場合は真の場合の値、満たさない場合は偽の場合の値を返します。ROW(セル)
セルの行番号を返します。何も指定しない場合はROWが書かれたセルの行番号を返します。 |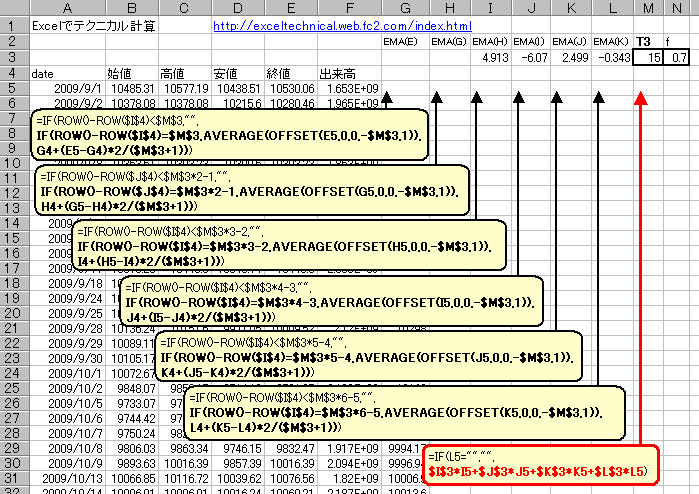
式を展開して計算します。
任意の日数のティルソンT3移動平均が計算できるようにOFFSET関数を使います。
計算式を作る前に3重のGeneralized DEMAを展開します。
N日Generalized DEMAはGDEMA(N)と表記することにします。
N日指数移動平均はEMA(N)と表記することにします。
M重N日指数移動平均はEMAM(N)と表記することにします。2重指数移動平均ならEMA2(N)、5重指数移動平均ならEMA5(N)となります。
2重GDEMAは
GDEMA(GDEMA(N)) = EMA(GDEMA(N))×(1+f)-EMA2(GDEMA(N))×f
=EMA(EMA(N)×(1+f)-EMA2(N))×(1+f)-EMA2(EMA(N)×(1+f)-EMA2(N)×f)×f
={EMA(EMA(N)×(1+f))-EMA(EMA2(N)×f)}×(1+f)-{EMA2(EMA(N)×(1+f))-EMA2(EMA2(N)×f)}×f
ここで
EMA(EMA(N))=EMA2(N), EMA(EMA2(N))=EMA3(N), EMA2(EMA(N))=EMA3(N), EMA2(EMA2(N))=EMA4(N)であり
関数内の係数は外にだすことができる、つまりEMA(EMA(N)×f)=EMA2(N)×fとできるので
上記の式を纏めると
GDEMA(GDEMA(N))=EMA2(N)×(1+f)^2 - EMA3(N)×f×(1+f) - EMA3(N)×f×(1+f) + EMA4(N)×f^2
=EMA2(N)×(1+f)^2 - 2×EMA3(N)×f×(1+f) + EMA4(N)×f^2
となります。
この形をよくみると(X-Y)^2の展開式をX=X×(1+f), Y=Y×fとして計算するのと同じ係数が得られることがわかります。
つまり、移動平均の式の展開はそれぞれの要素を簡単なX,Yなどでで置き換えて展開しても同じ係数が得られるということです。
上記の場合だと展開した後にX=EMA(N)、Y=EMA2(N)と置き換えてX^2=EMA(EMA(N))と解釈すれば同様の式が得られるということです。
よって、3重のGDEMAの展開式はX=EMA(N)、Y=EMA2(N)として、{X×(1+f)-Y×f}^3を展開すれば良いということになります。
{X×(1+f)-Y×f}^3を展開すると
X^3×(1+f)^3 - 3×X^2×Y×(1+f)^2×f + 3×X×Y^2×(1+f)×f^2 - Y^3×f^3
となり、X=EMA(N)、Y=EMA2(N)とすれば
EMA3(N)×(1+f)^3 - 3×EMA(4)×(1+f)^2×f + 3×EMA5(N)×(1+f)×f^2 - EMA6(N)×f^3
となります。
これで、準備が整いました。
M3セルはT3移動平均の計算日数を指定するセルとします。
N3セルはfを指定するセルとします。
G列で終値の指数移動平均を計算します。計算式の説明は指数移動平均を参照してください。
H列でG列の指数移動平均(2重指数移動平均)を計算します。同様にI列〜L列で3重〜6重の指数移動平均を計算します。
計算式はそれぞれ左隣の列の指数移動平均になっているので計算式の説明は省略します。
I3セルで3重指数移動平均の係数を計算します。
3重指数移動平均の係数は(1+f)^3で計算できるので式は=(1+N3)^3となります。
J3セルで4重指数移動平均の係数を計算します。
4重指数移動平均の係数は-3×(1+f)^2×fで計算できるので式は=-3*((1+N3)^2)*N3となります。
K3セルで5重指数移動平均の係数を計算します。
5重指数移動平均の係数は3×(1+f)×f^2で計算できるので式は=3*(1+N3)*(N3^2)となります。
L3セルで6重指数移動平均の係数を計算します。
6重指数移動平均の係数は-f^3で計算できるので式は=-N3^3となります。
M列でティルソンT3移動平均を計算します。
計算式はEMA3(N)×(1+f)^3 - 3×EMA(4)×(1+f)^2×f + 3×EMA5(N)×(1+f)×f^2 - EMA6(N)×f^3です。
各指数移動平均の数値はI列〜L列で、各指数移動平均の係数はI3セル〜L3セルで計算してあるので
Excelの式は赤枠内赤字部分
$I$3*I5+$J$3*J5+$K$3*K5+$L$3*L5
となります。G5〜M5セルをコピーしG6以下のセルにペーストすればティルソンT3移動平均が計算できます。
Excelファイルがダウンロードできない場合はリンクを右クリックして「対象をファイルに保存」を選択して保存すればダウンロードできます。
 自動売買ソフト W2C-Angely 
|
 FXファンド はじめ方・儲け方 
|
 ど素人がはじめる資産運用の本 
|
 デイトレード入門 第2版 短期売買の極意 
|
 2013年の日経平均株価の全予測と結果&2014年のシナリオ パワートレンド理論の実践 
|
 すごいシステムトレード
|
 完全レベル別30代〜50代のための海外投資「超」入門 
|
 ヘッジファンドで増やす時代 全天候型投資で儲ける
|
↑ TOP PAGE