2011/9/3
日経平均から計算したストキャスティックス%Dの度数分布
日経平均から計算したストキャスティックス%Dの度数分布について調べました。
日経平均についてストキャスティックス%Dの度数分布図を作りました。
用意したデータは1999/1/4〜2010/12/30の4本値です。
データ区間は2000/1/4〜2009/12/30の10年間を使います。
計算区間は2000/1/4よりもちょっと前から計算することになります。
度数分布はストキャスティックス%Dの計算結果をROUND関数で四捨五入し、0〜100までの101区間に振り分けます。
例えば、度数50の区間の範囲は49.5以上50.5未満というようになります。
だから、0の区間の範囲は、-0.5以上0.5未満、100の区間は99.5以上100.5未満ということになります。
ストキャスティックス%Dの計算結果は必ず0以上100以下になるので、0と100の区間だけ他の区間とは幅が狭くなるのですが、
切り上げ、切り捨てでは0か100のどちらかが極端に狭い範囲になるので、今回はこのようにして集計しています。
正規分布とは違う分布になりました。
ストキャスティックス%Dの計算日数を変えてみます。
今回は変数が2つになります。まずはストキャスティックス%Kと共通する変数(最高値や最安値の計算区間を設定する変数)を変えてみます。
計算日数を長くした場合(50日、3日)
計算日数を短くした場合(4日、3日)
長くしても短くしても正規分布にはならないようです。
次にストキャスティックス%D独自の変数(移動平均の区間を設定する変数)を変えてみます。
計算日数を長くした場合(14日、50日)
計算日数を短くした場合(14日、1日)
両方の変数を変えるとこういう分布が得られます。
(4日、50日)の場合
次に、期間内での数値に偏りがあるかどうか調べるために、データ区間を2年ごとに区切り、
重ねて表示してみます。
それ以外では空色の右端寄りが目立ち、その他の分布にはあまり差異は見られません。
度数分布の場合と同様に変数を動かしてみます。
(50日、3日)の場合が以下の図です。
全体的に(14日、3日)の傾向と変わらないように見えます。
(4日、3日)の場合
(14日、50日)の場合
(14日、1日)の場合
(4日、50日)の場合
まとめ
日経平均についてストキャスティックス%Dの度数分布図を作りました。
用意したデータは1999/1/4〜2010/12/30の4本値です。
データ区間は2000/1/4〜2009/12/30の10年間を使います。
計算区間は2000/1/4よりもちょっと前から計算することになります。
度数分布はストキャスティックス%Dの計算結果をROUND関数で四捨五入し、0〜100までの101区間に振り分けます。
例えば、度数50の区間の範囲は49.5以上50.5未満というようになります。
だから、0の区間の範囲は、-0.5以上0.5未満、100の区間は99.5以上100.5未満ということになります。
ストキャスティックス%Dの計算結果は必ず0以上100以下になるので、0と100の区間だけ他の区間とは幅が狭くなるのですが、
切り上げ、切り捨てでは0か100のどちらかが極端に狭い範囲になるので、今回はこのようにして集計しています。
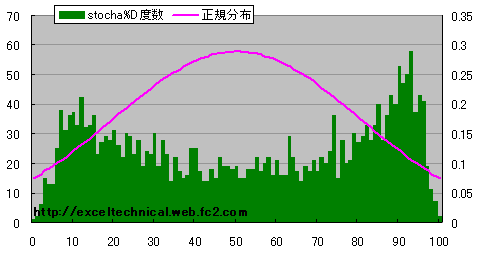 |
日経平均 ストキャスティックス%D度数分布図(14日、3日)
緑が度数を示し、ピンクの線はデータ区間から標準偏差を計算し、その数値から正規分布を計算したものです。正規分布とは違う分布になりました。
ストキャスティックス%Dの計算日数を変えてみます。
今回は変数が2つになります。まずはストキャスティックス%Kと共通する変数(最高値や最安値の計算区間を設定する変数)を変えてみます。
計算日数を長くした場合(50日、3日)
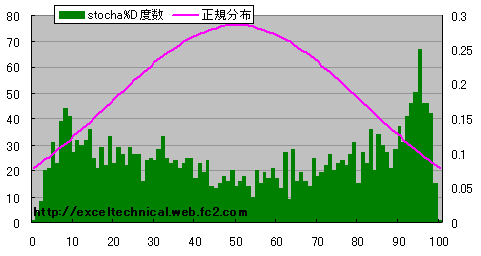 |
日経平均 ストキャスティックス%D度数分布図(50日、3日)
計算日数を短くした場合(4日、3日)
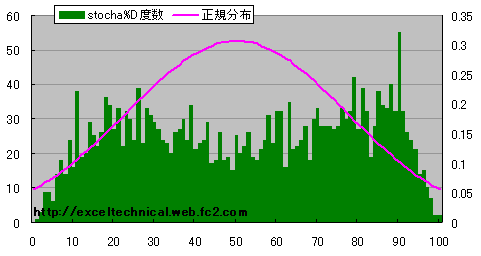 |
日経平均 ストキャスティックス%D度数分布図(4日、3日)
若干の変化は見られますが、分布の形そのものに変化は無いようです。長くしても短くしても正規分布にはならないようです。
次にストキャスティックス%D独自の変数(移動平均の区間を設定する変数)を変えてみます。
計算日数を長くした場合(14日、50日)
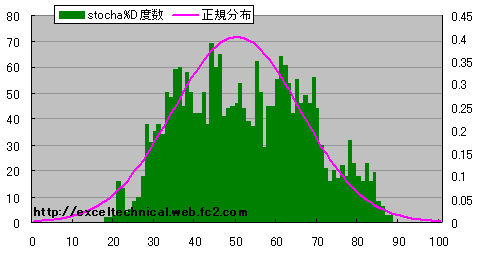 |
日経平均 ストキャスティックス%D度数分布図(14日、50日)
分布の形が変化し、中央付近の分布が多くなりました。計算日数を短くした場合(14日、1日)
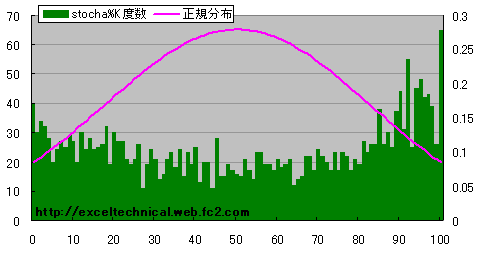 |
日経平均 ストキャスティックス%D度数分布図(14日、1日)
1日の場合はストキャスティックス%Kを14日で計算した場合と同様になります。両方の変数を変えるとこういう分布が得られます。
(4日、50日)の場合
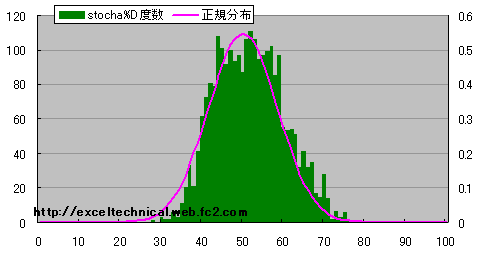 |
日経平均 ストキャスティックス%D度数分布図(4日、50日)
正規分布とは言えないまでも、それに近い分布が得られる変数の組み合わせもあります。次に、期間内での数値に偏りがあるかどうか調べるために、データ区間を2年ごとに区切り、
重ねて表示してみます。
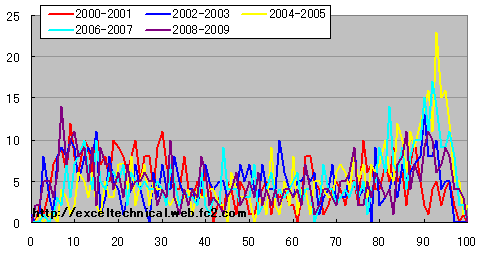 |
日経平均 ストキャスティックス%D度数分布図(14日、3日) 2年区切り
上昇相場が長かった2004-2005年(図中では黄色のライン)は90〜100の間に近傍にピークがあります。それ以外では空色の右端寄りが目立ち、その他の分布にはあまり差異は見られません。
度数分布の場合と同様に変数を動かしてみます。
(50日、3日)の場合が以下の図です。
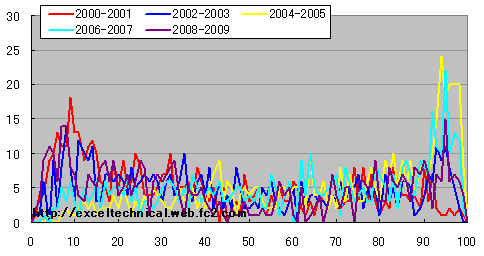 |
日経平均 ストキャスティックス%D度数分布図(50日、3日) 2年区切り
黄色のラインの分布がかなり目立ちます。赤のラインは左の度数が多くなりました。全体的に(14日、3日)の傾向と変わらないように見えます。
(4日、3日)の場合
 |
日経平均 ストキャスティックス%D度数分布図(4日、3日) 2年区切り
分布の形に変化は見られませんが、区間ごとの度数の差が小さくなり、期間毎の差が目立たなくなりました。(14日、50日)の場合
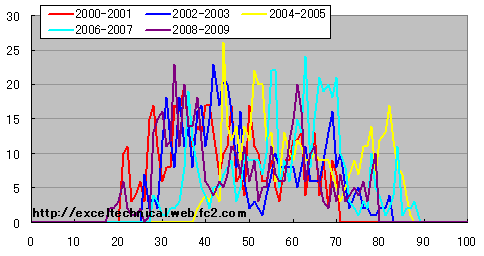 |
日経平均 ストキャスティックス%D度数分布図(14日、50日) 2年区切り
黄色と空色が右シフト、赤が左シフトしています。(14日、1日)の場合
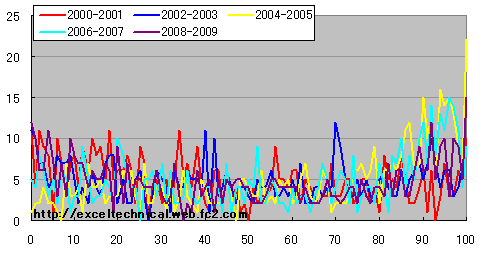 |
日経平均 ストキャスティックス%D度数分布図(14日、1日) 2年区切り
これはストキャスティックス%K14日と同様の分布になります。(4日、50日)の場合
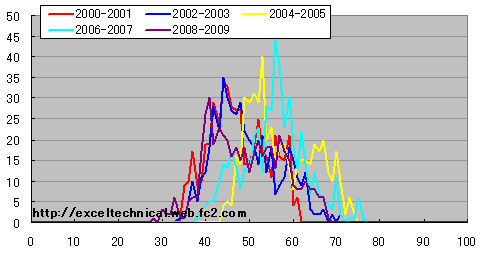 |
日経平均 ストキャスティックス%D度数分布図(4日、50日) 2年区切り
各期間の傾向は(14日、50日)と同様ですがより中央に寄っています。まとめ
ストキャスティックス%Dの分布は両端近傍にピークを持ち中央が凹んだ形になることが多い。
ストキャスティックス%Kと共通の変数の計算期間を長くしても分布の形に大きな変化は見られない。
移動平均を決める変数を動かすと分布に変化が見られる。
ストキャスティックス%Dの度数分布は正規分布ではないが、変数の設定によって正規分布に近い分布を得ることができる。
ストキャスティックス%Kと共通の変数の計算期間を長くしても分布の形に大きな変化は見られない。
移動平均を決める変数を動かすと分布に変化が見られる。
ストキャスティックス%Dの度数分布は正規分布ではないが、変数の設定によって正規分布に近い分布を得ることができる。
|
|
|
|
|
|
|
|
|
|
↑ TOP PAGE







