2011/12/10
Morris RSIの度数分布(日経平均)
Morris RSIの度数分布について調べてみました。
日経平均のMorris RSIの度数分布図を作りました。
用意したデータは1999/1/4〜2010/12/30の4本値です。
Morris RSIのデータは2000/1/4〜2009/12/30の10年間を使います。
度数分布はMorris RSIの計算結果をROUND関数で四捨五入し、0〜100までの101区間に振り分けます。
つまり、度数50の区間の範囲は49.5以上50.5未満というようになります。
だから、0の区間の範囲は、-0.5以上0.5未満、100の区間は99.5以上100.5未満ということになります。
Morris RSIの計算結果は必ず0以上100以下になるので、0と100の区間だけ他の区間とは幅が狭くなるのですが、
切り上げ、切り捨てでは0か100のどちらかが極端に狭い範囲になるので、今回はこのようにして集計しています。
正規分布に近い分布になるようです。
これだけではよくわからないので計算日数を変えてみます。
計算日数を長くした場合(50日)
計算日数を短くした場合(4日)
ピーク位置は中央から左側にずれました。
4日の方は0近傍、100近傍の度数が著しく増加しそれ以外の分布が一様になります。こちらはRSIの挙動と同じようです。
次に、期間内での数値に偏りがあるかどうか調べるために、データ区間を2年ごとに区切り、
重ねて表示してみます。
50日の場合が以下の図です。
50〜70の間に小さいピークがあるようにも見えます。
4日の場合を見てみます。
まとめ
日経平均のMorris RSIの度数分布図を作りました。
用意したデータは1999/1/4〜2010/12/30の4本値です。
Morris RSIのデータは2000/1/4〜2009/12/30の10年間を使います。
度数分布はMorris RSIの計算結果をROUND関数で四捨五入し、0〜100までの101区間に振り分けます。
つまり、度数50の区間の範囲は49.5以上50.5未満というようになります。
だから、0の区間の範囲は、-0.5以上0.5未満、100の区間は99.5以上100.5未満ということになります。
Morris RSIの計算結果は必ず0以上100以下になるので、0と100の区間だけ他の区間とは幅が狭くなるのですが、
切り上げ、切り捨てでは0か100のどちらかが極端に狭い範囲になるので、今回はこのようにして集計しています。
 |
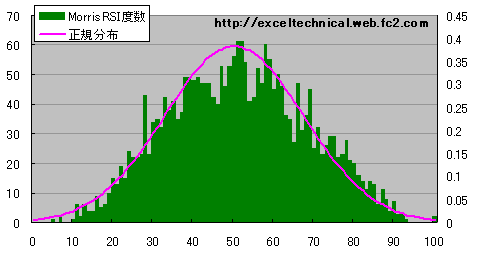日経平均 Morris RSI度数分布図(14日)
緑が度数を示し、ピンクの線はデータ区間から標準偏差を計算し、その数値から正規分布を計算したものです。正規分布に近い分布になるようです。
これだけではよくわからないので計算日数を変えてみます。
計算日数を長くした場合(50日)
 |
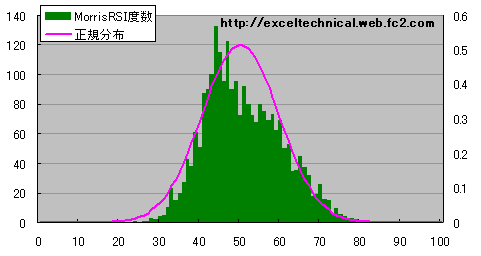日経平均 Morris RSI度数分布図(50日)
計算日数を短くした場合(4日)
 |
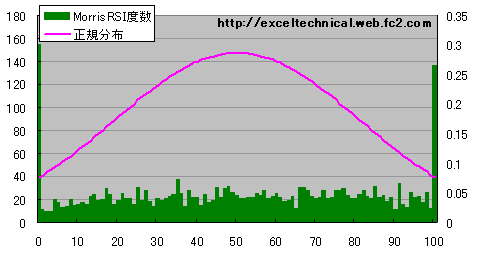日経平均 Morris RSI度数分布図(4日)
計算日数を長く取ると分布が狭くなります。ピーク位置は中央から左側にずれました。
4日の方は0近傍、100近傍の度数が著しく増加しそれ以外の分布が一様になります。こちらはRSIの挙動と同じようです。
次に、期間内での数値に偏りがあるかどうか調べるために、データ区間を2年ごとに区切り、
重ねて表示してみます。
 |
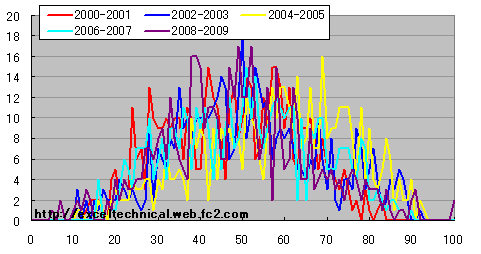日経平均 Morris RSI度数分布図(14日) 2年区切り
黄色(2004-2005年)が右にシフトしています。50日の場合が以下の図です。
 |
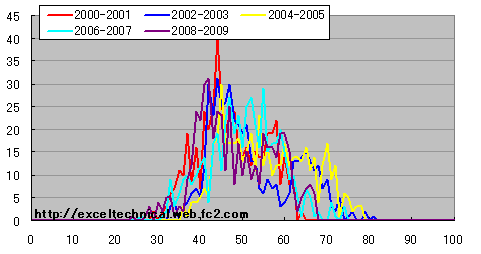日経平均 Morris RSI度数分布図(50日) 2年区切り
空色以外の色のピーク位置が40付近にあります。50〜70の間に小さいピークがあるようにも見えます。
4日の場合を見てみます。
 |
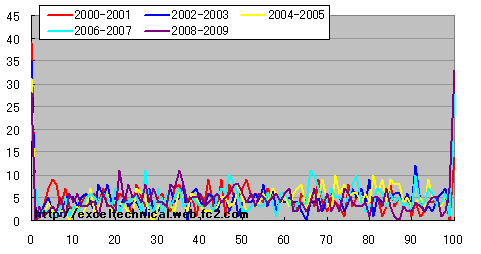日経平均 Morris RSI度数分布図(4日) 2年区切り
4日では期間ごとの偏りは見えませんでした。まとめ
Morris RSIの挙動はRSIに似ている。
Morris RSIは14日前後の計算期間では度数分布が正規分布に近くなる。
計算期間を長くすると分布が狭くなる。
極端に短くすると0近傍、100近傍の値を取りやすくなり、それ以外の値はほぼ一様に分布するようになる。
Morris RSIは14日前後の計算期間では度数分布が正規分布に近くなる。
計算期間を長くすると分布が狭くなる。
極端に短くすると0近傍、100近傍の値を取りやすくなり、それ以外の値はほぼ一様に分布するようになる。
 できるポケット Excelグラフ 基本マスターブック 2013/2010対応 
|
 今すぐ使えるかんたんmini Word & Excel & PowerPoint & Outlook 2013 基本技 
|
 英語教育学の実証的研究法入門 ――Excelで学ぶ統計処理 
|
 Excelで学ぶ共分散構造分析とグラフィカルモデリング―Excel2013/2010/2007対応版― 
|
 よくわかるマスター MOS Excel 2013対策テキスト(CD-ROM無し) (FOM出版のみどりの本) 
|
 できる逆引き Excel VBAを極める勝ちワザ700 2016/2013/2010/2007対応 
|
 基礎から学ぶ統計解析 −Excel 2010対応−
|
 なぜ、あなたのExcelは「パッとしない」のか? いまさら聞けない社会人のための再入門 
|
↑ TOP PAGE