2011/9/19
Distance Coefficient
John F. Ehlersが開発した移動平均で加重移動平均の一種です。
加重が値動きの距離に相関するように調整されており、収束が早いことが特徴です。
使用する関数
引数となる配列は行数と列数が等しい配列である必要があります。行数と列数が等しくない場合、エラー値 #VALUE! が返されます。
Distance Coefficientは加重移動平均の一種ですが加重であるcoefの計算が面倒です。
coefの計算は計算式とは少々異なる方法で計算するのでその説明を行ってから、計算式の説明をします。
coefは(P-P1)の2乗+(P-P2)の2乗+(P-P3)の2乗+…というように計算するのですが、
Excelではこのような計算を直接計算するような関数が無いので、似たような計算を行う関数を使うことにします。
DEVSQという関数がそれにあたります。この関数は引数の平均を計算し、その平均値からの各引数の差の2乗の和を計算します。
つまり、DEVSQ(X,Y,Z)とすると、X,Y,Zの平均値をMとして
(M-X)^2+(M-Y)^2+(M-Z)^2が返されます。
ここではこの関数を利用してcoefを計算します。
DEVSQ関数は内部で平均値を計算するのですが、この平均値と直近中値が同じ値になるように調整する値を引数で与えて
計算された値からこの値と直近中値との差の2乗を引けばcoefが計算できます。
式で考えてみます。直近中値をPとして、前日〜3日前の値をX,Y,Zとします。
DEVSQ(P,X,Y,Z)は内部でM=(P+X+Y+Z)/4を計算し
(M-P)^2+(M-X)^2+(M-Y)^2+(M-Z)^2を値として返してきます。
ここでM=Pとなるような数字Aを計算してDEVSQ(A,X,Y,Z)を計算してみます。
DEVSQ(A,X,Y,Z)は内部でM=(A+X+Y+Z)/4を計算し
(M-A)^2+(M-X)^2+(M-Y)^2+(M-Z)^2を値として返してきます。[1]
ここでAはM=Pとなるような数字と定義してありますからAは
P=(A+X+Y+Z)/4
A=4P-(X+Y+Z) [2]
で計算される数字です。
また、M=Pになるわけですから
[1]の式、つまりDEVSQ(A,X,Y,Z)で計算された値は
(P-A)^2+(P-X)^2+(P-Y)^2+(P-Z)^2 [3]
となります。ここで計算したかった値は
(P-X)^2+(P-Y)^2+(P-Z)^2なので
[3]の式から(P-A)^2を引けば計算できます。
つまりDEVSQ(A,X,Y,Z)-(P-A)^2でPとX,Y,Zそれぞれの差の2乗の和が計算できるわけです。
Aは[2]の式でわかるようにP,X,Y,Zから計算できるのでDEVSQを使って任意の値からの距離が計算できるということになります。
ここでは上記の計算をH列とI列を使って行っています。
ここから計算式の説明に入ります。
H4セルはDistance Coefficientの計算日数を指定するセルとします。
G列で中値を計算します。簡単な計算式なので説明は省略します。
H列とI列でcoefを計算します。DEVSQ関数を使ってcoefを計算する原理は上記の通りです。
上記の説明のAを計算している部分がH列で、I列でその値を使ってcoefを計算しています。
それぞれの計算式は
H列
I列
J列でDistance Coefficientを計算します。計算式は加重移動平均の計算式と構造は同じです。
計算式は赤枠内赤字部分
G5〜J5セルをコピーしG6以下のセルにペーストすればDistance Coefficientが計算できます。
Excelファイルがダウンロードできない場合はリンクを右クリックして「対象をファイルに保存」を選択して保存すればダウンロードできます。
加重が値動きの距離に相関するように調整されており、収束が早いことが特徴です。
計算式
中値 = (高値 + 安値) ÷ 2
coef = 直近中値と前日までのN日間各中値との差の2乗和
つまり直近中値をPとして、前日中値をP1、2日前をP2、3日前をP3とすると
coef = (P - P1)の2乗 + (P - P2)の2乗 + (P - P3)の2乗という計算になります
DC = (coef × 中値)のN日総和 ÷ coefのN日総和
Nは任意 EhlersはN=15を推奨
coef = 直近中値と前日までのN日間各中値との差の2乗和
つまり直近中値をPとして、前日中値をP1、2日前をP2、3日前をP3とすると
coef = (P - P1)の2乗 + (P - P2)の2乗 + (P - P3)の2乗という計算になります
DC = (coef × 中値)のN日総和 ÷ coefのN日総和
Nは任意 EhlersはN=15を推奨
 |
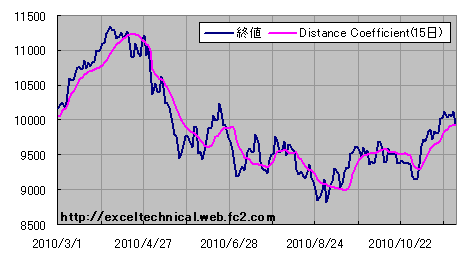日経平均終値とDistance Coefficientの図
Excelを使ってDistance Coefficientを計算する
Excelを使ってDistance Coefficientを計算する手順を説明します。使用する関数
DEVSQ(数値1,数値2,…)
引数の平均値からの差の2乗の和を計算します。SUMPRODUCT(配列 1,配列 2,配列 3,…)
引数として指定した配列の対応する要素間の積をまず計算し、さらにその和を返します。引数となる配列は行数と列数が等しい配列である必要があります。行数と列数が等しくない場合、エラー値 #VALUE! が返されます。
SUM(数値1,数値2,…)
引数の合計を計算します。OFFSET(基準セル,行数,列数,高さ,幅)
基準セルから指定した行数、列数だけ移動したセルを参照します。または高さ、幅を設定して基準セルから指定した高さ、幅のセル範囲を指定します。IF(条件式,真の場合,偽の場合)
条件式を満たす場合は真の場合の値、満たさない場合は偽の場合の値を返します。ROW(セル)
セルの行番号を返します。何も指定しない場合はROWが書かれたセルの行番号を返します。 |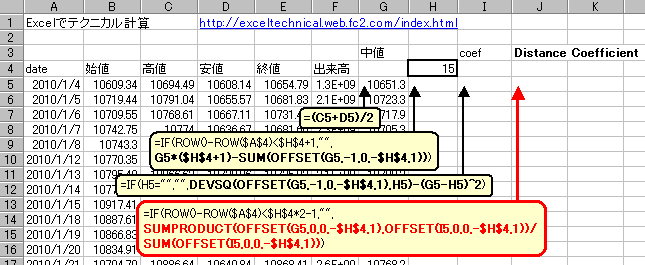
coefの計算は計算式とは少々異なる方法で計算するのでその説明を行ってから、計算式の説明をします。
coefは(P-P1)の2乗+(P-P2)の2乗+(P-P3)の2乗+…というように計算するのですが、
Excelではこのような計算を直接計算するような関数が無いので、似たような計算を行う関数を使うことにします。
DEVSQという関数がそれにあたります。この関数は引数の平均を計算し、その平均値からの各引数の差の2乗の和を計算します。
つまり、DEVSQ(X,Y,Z)とすると、X,Y,Zの平均値をMとして
(M-X)^2+(M-Y)^2+(M-Z)^2が返されます。
ここではこの関数を利用してcoefを計算します。
DEVSQ関数は内部で平均値を計算するのですが、この平均値と直近中値が同じ値になるように調整する値を引数で与えて
計算された値からこの値と直近中値との差の2乗を引けばcoefが計算できます。
式で考えてみます。直近中値をPとして、前日〜3日前の値をX,Y,Zとします。
DEVSQ(P,X,Y,Z)は内部でM=(P+X+Y+Z)/4を計算し
(M-P)^2+(M-X)^2+(M-Y)^2+(M-Z)^2を値として返してきます。
ここでM=Pとなるような数字Aを計算してDEVSQ(A,X,Y,Z)を計算してみます。
DEVSQ(A,X,Y,Z)は内部でM=(A+X+Y+Z)/4を計算し
(M-A)^2+(M-X)^2+(M-Y)^2+(M-Z)^2を値として返してきます。[1]
ここでAはM=Pとなるような数字と定義してありますからAは
P=(A+X+Y+Z)/4
A=4P-(X+Y+Z) [2]
で計算される数字です。
また、M=Pになるわけですから
[1]の式、つまりDEVSQ(A,X,Y,Z)で計算された値は
(P-A)^2+(P-X)^2+(P-Y)^2+(P-Z)^2 [3]
となります。ここで計算したかった値は
(P-X)^2+(P-Y)^2+(P-Z)^2なので
[3]の式から(P-A)^2を引けば計算できます。
つまりDEVSQ(A,X,Y,Z)-(P-A)^2でPとX,Y,Zそれぞれの差の2乗の和が計算できるわけです。
Aは[2]の式でわかるようにP,X,Y,Zから計算できるのでDEVSQを使って任意の値からの距離が計算できるということになります。
ここでは上記の計算をH列とI列を使って行っています。
ここから計算式の説明に入ります。
H4セルはDistance Coefficientの計算日数を指定するセルとします。
G列で中値を計算します。簡単な計算式なので説明は省略します。
H列とI列でcoefを計算します。DEVSQ関数を使ってcoefを計算する原理は上記の通りです。
上記の説明のAを計算している部分がH列で、I列でその値を使ってcoefを計算しています。
それぞれの計算式は
H列
G5*($H$4+1)-SUM(OFFSET(G5,-1,0,-$H$4,1))
I列
DEVSQ(OFFSET(G5,-1,0,-$H$4,1),H5)-(G5-H5)^2
となります。J列でDistance Coefficientを計算します。計算式は加重移動平均の計算式と構造は同じです。
計算式は赤枠内赤字部分
SUMPRODUCT(OFFSET(G5,0,0,-$H$4,1),OFFSET(I5,0,0,-$H$4,1))/SUM(OFFSET(I5,0,0,-$H$4,1))
となります。G5〜J5セルをコピーしG6以下のセルにペーストすればDistance Coefficientが計算できます。
Excelファイルがダウンロードできない場合はリンクを右クリックして「対象をファイルに保存」を選択して保存すればダウンロードできます。
 テクニカル分析 Σ3級コース 
|
 シュワッガーのマーケット教室 
|
 6日で完全マスターFX入門 かんたんスタンダードガイド 
|
 先物の世界 相場開眼 
|
 デリバティブ用語辞典 
|
 まずは副業で月10万！FXチャート最強実戦集
|
 毎月1回10分チェックで年20％らくらく儲かる 景気ウォッチャー投資法入門
|
 行動ファイナンス 市場の非合理性を解き明かす新しい金融理論 
|
↑ TOP PAGE