2011/4/16
ALMA(Arnaud Legoux Moving Average)
ALMA(Arnaud Legoux Moving Average)はArnaud LegouxとDimitrios Kouzis Loukasによって開発された移動平均です。
加重移動平均の一種で、係数の形がガウシアンフィルターになっています。
通常のガウシアンフィルターは中央が最も高い左右対称の釣鐘型ですが、ALMAではピークを直近にずらした非対称のガウシアンフィルターを
使うことで、価格への追随性を改善しています。
使用する関数
引数となる配列は行数と列数が等しい配列である必要があります。行数と列数が等しくない場合、エラー値 #VALUE! が返されます。
ALMAは加重移動平均の一種なので、係数を先に計算してSUMPRODUCT関数を使ってALMAを計算します。
ここでは任意の日数のALMAが計算できるようにOFFSET関数を使います。
H4セルはALMAの計算日数を指定するセルとします。
I2セルは変数Aを指定するセルとします。
I3セルは変数Bを指定するセルとします。
G4セルでoffsetを計算します。offsetはB×(計算日数-1)の切り捨てなので 計算式は
I5セルでσを計算します。σは計算日数÷Aで計算されます。簡単な計算式なので式の説明は省略します。
G列で係数を計算します。
係数はexp{-(i-offset)の2乗/σの2乗}で計算されます。
ここで面倒なのが(i-offset)のiの部分です。iは計算開始が1で1行下がるごとに+1される数列です。
この数列はrow関数で実現できるので、これを使って係数の数式をExcelの式に直すと
H列でALMAを計算します。
計算式は加重移動平均と同じ式になります。
計算式の部分は赤枠内赤字部です。計算式が2行になっていて見にくいので書き出すと
G5,H5セルをコピーし、G6以下のセルにペーストすればArnaud Legoux Moving Averageが計算できます。
Excelファイルがダウンロードできない場合はリンクを右クリックして「対象をファイルに保存」を選択して保存すればダウンロードできます。
加重移動平均の一種で、係数の形がガウシアンフィルターになっています。
通常のガウシアンフィルターは中央が最も高い左右対称の釣鐘型ですが、ALMAではピークを直近にずらした非対称のガウシアンフィルターを
使うことで、価格への追随性を改善しています。
計算式
ALMA =Σ(CiXi)/Σ(Xi)
Ci(i=1,2,3,…,N)は各終値
Xi(i=1,2,3,…,N)は各終値に係る任意の係数
Xi = exp{-(i - offset)の2乗/σの2乗}
σ = N ÷ A
offset ={ B × (N - 1)}の切り捨て
A,B,Nは任意 A=6,B=0.85がデフォルト
Ci(i=1,2,3,…,N)は各終値
Xi(i=1,2,3,…,N)は各終値に係る任意の係数
Xi = exp{-(i - offset)の2乗/σの2乗}
σ = N ÷ A
offset ={ B × (N - 1)}の切り捨て
A,B,Nは任意 A=6,B=0.85がデフォルト
 |
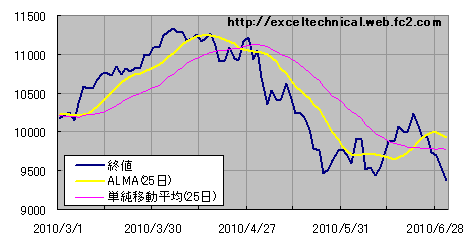日経平均終値とArnaud Legoux Moving Averageの図
Excelを使ってArnaud Legoux Moving Averageを計算する
Excelを使ってArnaud Legoux Moving Averageを計算する手順を説明します。使用する関数
TRUNC(数値)
指定した数値の小数点以下を切り捨てます。EXP(数値)
eを底とする数値の冪乗を返します。ROW(セル)
セルの行番号を返します。何も指定しない場合はROWが書かれたセルの行番号を返します。SUMPRODUCT(配列 1,配列 2,配列 3,…)
引数として指定した配列の対応する要素間の積をまず計算し、さらにその和を返します。引数となる配列は行数と列数が等しい配列である必要があります。行数と列数が等しくない場合、エラー値 #VALUE! が返されます。
SUM(数値1,数値2,…)
引数の合計を計算します。OFFSET(基準セル,行数,列数,高さ,幅)
基準セルから指定した行数、列数だけ移動したセルを参照します。または高さ、幅を設定して基準セルから指定した高さ、幅のセル範囲を指定します。IF(条件式,真の場合,偽の場合)
条件式を満たす場合は真の場合の値、満たさない場合は偽の場合の値を返します。 |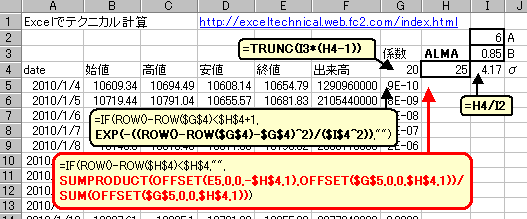
ここでは任意の日数のALMAが計算できるようにOFFSET関数を使います。
H4セルはALMAの計算日数を指定するセルとします。
I2セルは変数Aを指定するセルとします。
I3セルは変数Bを指定するセルとします。
G4セルでoffsetを計算します。offsetはB×(計算日数-1)の切り捨てなので 計算式は
=TRUNC(I3*(H4-1))
となります。I5セルでσを計算します。σは計算日数÷Aで計算されます。簡単な計算式なので式の説明は省略します。
G列で係数を計算します。
係数はexp{-(i-offset)の2乗/σの2乗}で計算されます。
ここで面倒なのが(i-offset)のiの部分です。iは計算開始が1で1行下がるごとに+1される数列です。
この数列はrow関数で実現できるので、これを使って係数の数式をExcelの式に直すと
EXP(-((ROW()-ROW($G$4)-$G$4)^2)/($I$4^2))
となります。H列でALMAを計算します。
計算式は加重移動平均と同じ式になります。
計算式の部分は赤枠内赤字部です。計算式が2行になっていて見にくいので書き出すと
SUMPRODUCT(OFFSET(E5,0,0,-$H$4,1),OFFSET($G$5,0,0,$H$4,1))/SUM(OFFSET($G$5,0,0,$H$4,1))
となります。G5,H5セルをコピーし、G6以下のセルにペーストすればArnaud Legoux Moving Averageが計算できます。
Excelファイルがダウンロードできない場合はリンクを右クリックして「対象をファイルに保存」を選択して保存すればダウンロードできます。
 金融工学20年-20世紀エンジニアの冒険 
|
 勝利の売買システム トレードステーションから学ぶ実践的売買プログラミング 
|
 うねり取り株式投資法 基本と実践 
|
 第四巻 わが最上の型譜 
|
 FX常勝の平均足ブレイクトレード 
|
 やっぱりすごいぞ！株のデイトレ
|
 百人百色の投資法 Vol.4
|
 世界No.1投資家バフェットの謎 何がその成功をもたらしたのか?
|
↑ TOP PAGE